Buddhabrot fractals

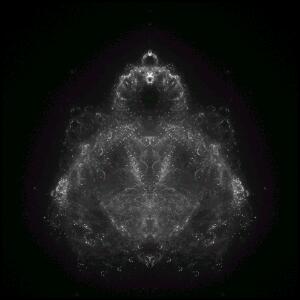
The Buddhabrot was discovered by Melinda Green, who adapted the classical Mandelbrot set algorithm to develop a new way of displaying it.
Lori Gardi named this rendering the "Buddhabrot".

In the classical approach, each pixel goes through the Mandelbrot formula. A point can escape or not escape after a certain number of iterations. The pixel is then plotted.

In the Buddhabrot approach, one selects points in the sample area of the complex number plane (-2 to 2 in both x and y direction, for example). The Mandelbrot formula is used without plotting to test if the point escapes to infinity or not.

if the point does not escape, one choses another random point (i.e. the points inside the Mandelbrot set are ignored)
if the point escapes, the iterated formula is run a second time, and all the intermediate points are plotted

Melinda's method is to choose random points from the sample area, Lori Gardi proposed to use an ordered grid to step though the sample area, I've employed the ordered grid method in the program I used to render the Buddhabrot fractals shown here.

Buddhabrot Maker (DOS/console, compiled QBasic program) info, screenshots and download

91.66 KB	52.85 KB	99.81 KB
164.47 KB	140.38 KB	167.07 KB

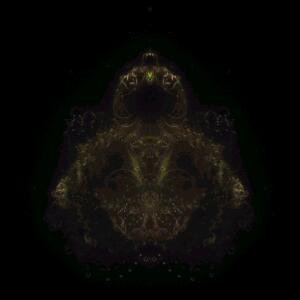
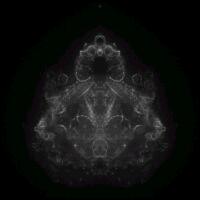
The lower three images are a variation on the Buddhabrot method, which uses the points that do not escape (the points inside the M-set) instead of the points that escape. The result is similar to the Mandelcloud type fractal in Fractint with Outside=Summ.

Buddhabrot links (updated januari 8 2005)

To Fractal Expo index
To site index